Estimadores Media poblacional

Estimadores
Ejercicio en clases
25+15.53.88=40.5388
25-15.5388=9.4612

9.4612<M<40.5388

ESTIMADORES

 Características estimadores

1) Sesgo. Se dice que un estimador es insesgado si la Media de la distribución del estimador es igual al parámetro.

Estimadores insesgados son la Media muestral (estimador de la Media de la población) y la Varianza (estimador de la Varianza de la población):

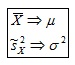
Ejemplo

En una población de 500 puntuaciones cuya Media (m) es igual a 5.09 han hecho un muestreo aleatorio (número de muestras= 10000, tamaño de las muestras= 100) y hallan que la Media de las Medias muestrales es igual a 5.09, (la media poblacional y la media de las medias muestrales coinciden). En cambio, la Mediana de la población es igual a 5 y la Media de las Medianas es igual a 5.1 esto es, hay diferencia ya que la Mediana es un estimador sesgado.

La Varianza es un estimador sesgado. Ejemplo: La Media de las Varianzas obtenidas con la Varianza

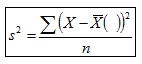
en un muestreo de 1000 muestras (n=25) en que la Varianza de la población es igual a 9.56ha resultado igual a 9.12, esto es, no coinciden. En cambio, al utilizar la Cuasivarianza

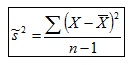
la Media de las Varianzas muestrales es igual a 9.5, esto es, coincide con la Varianza de la población ya que la Cuasivarianza es un estimador insesgado.

2) Consistencia. Un estimador es consistente si aproxima el valor del parámetro cuanto mayor es n (tamaño de la muestra).

Algunos estimadores consistentes son:

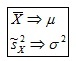
Ejemplo

En una población de 500 puntuaciones cuya Media (m) es igual a 4.9 han hecho tres muestreos aleatorios (número de muestras= 100) con los siguientes resultados:

vemos que el muestreo en que n=100 la Media de las Medias muestrales toma el mismo valor que la Media de la población.

3) Eficiencia. Diremos que un estimador es más eficiente que otro si la Varianza de la distribución muestral del estimador es menor a la del otro estimador. Cuanto menor es la eficiencia, menor es la confianza de que el estadístico obtenido en la muestra aproxime al parámetro poblacional.

Ejemplo

La Varianza de la distribución muestral de la Media en un muestreo aleatorio (número de muestras: 1000, n=25) ha resultado igual a 0.4. La Varianza de la distribución de Medianas ha resultado, en el mismo muestreo, igual a 1.12, (este resultado muestra que la Media es un estimador más eficiente que la Mediana).

DISTRIBUCION DE T DE STUDENT

DISTRIBUCION "T DE STUDENT"

Supóngase que se toma una muestra de una población normal con media  y varianza . Si es el promedio de las n observaciones que contiene la muestra aleatoria, entonces la distribución  es una distribución normal estándar. Supóngase que la varianza de la población ² es desconocida. ¿Qué sucede con la distribución de esta estadística si se reemplaza  por s? La distribución t proporciona la respuesta a esta pregunta.

La media y la varianza de la distribución t son  = 0 y  para >2, respectivamente.

La siguiente figura presenta la gráfica de varias distribuciones t. La apariencia general de la distribución t es similar a la de la distribución normal estándar: ambas son simétricas y unimodales, y el valor máximo de la ordenada se alcanza en la media  = 0. Sin embargo, la distribución t tiene colas más amplias que la normal; esto es, la probabilidad de las colas es mayor que en la distribución normal. A medida que el número de grados de libertad tiende a infinito, la forma límite de la distribución t es la distribución normal estándar.

Propiedades de las distribuciones t

1. Cada curva t tiene forma de campana con centro en 0.



2. Cada curva t, está más dispersa que la curva normal estándar z.


3. A medida que  aumenta, la dispersión de la curva t correspondiente disminuye.


4. A medida que  , la secuencia de curvas t se aproxima a la curva normal estándar, por lo que la curva z recibe a veces el nombre de curva t con gl = 

La distribución de la variable aleatoria t está dada por:

Esta se conoce como la distribución t con  grados de libertad.

Sean X₁, X₂, . . . , X_n variables aleatorias independientes que son todas normales con media  y desviación estándar . Entonces la variable aleatoria  tiene una distribución t con  = n-1 grados de libertad.

La distribución de probabilidad de t se publicó por primera vez en 1908 en un artículo de W. S. Gosset. En esa época, Gosset era empleado de una cervecería irlandesa que desaprobaba la publicación de investigaciones de sus empleados. Para evadir esta prohibición, publicó su trabajo en secreto bajo el nombre de "Student". En consecuencia, la distribución t normalmente se llama distribución t de Student, o simplemente distribución t. Para derivar la ecuación de esta distribución, Gosset supone que las muestras se seleccionan de una población normal. Aunque esto parecería una suposición muy restrictiva, se puede mostrar que las poblaciones no normales que poseen distribuciones en forma casi de campana aún proporcionan valores de t que se aproximan muy de cerca a la distribución t.

La distribución t difiere de la de Z en que la varianza de t depende del tamaño de la muestra y siempre es mayor a uno. Unicamente cuando el tamaño de la muestra tiende a infinito las dos distribuciones serán las mismas.

Se acostumbra representar con el valor t por arriba del cual se encuentra un área igual a . Como la distribución t es simétrica alrededor de una media de cero, tenemos; es decir, el valor t que deja un área de  a la derecha y por tanto un área de  a la izquierda, es igual al valor t negativo que deja un área de  en la cola derecha de la distribución. Esto es, t_0.95 = -t_0.05, t_0.99=-t_0.01, etc.

Para encontrar los valores de t se utilizará la tabla de valores críticos de la distribución t del libro Probabilidad y Estadística para Ingenieros de los autores Walpole, Myers y Myers.

Ejemplo:

El valor t con  = 14 grados de libertad que deja un área de 0.025 a la izquierda, y por tanto un área de 0.975 a la derecha, es

t_0.975=-t_0.025 = -2.145

Si se observa la tabla, el área sombreada de la curva es de la cola derecha, es por esto que se tiene que hacer la resta de . La manera de encontrar el valor de t es buscar el valor de  en el primer renglón de la tabla y luego buscar los grados de libertad en la primer columna y donde se intercepten  y  se obtendrá el valor de t.

Ejemplo:
Encuentre la probabilidad de –t_0.025 < t < t_0.05.
Solución:

Como t_0.05 deja un área de 0.05 a la derecha, y –t_0.025 deja un área de 0.025 a la izquierda, encontramos un área total de 1-0.05-0.025 = 0.925.

P( –t_0.025 < t < t_0.05) = 0.925

Ejemplo:
Encuentre k tal que P(k < t < -1.761) = 0.045, para una muestra aleatoria de tamaño 15 que se selecciona de una distribución normal.
Solución:

Si se busca en la tabla el valor de t =1.761 con 14 grados de libertad nos damos cuenta que a este valor le corresponde un área de 0.05 a la izquierda, por ser negativo el valor. Entonces si se resta 0.05 y 0.045 se tiene un valor de 0.005, que equivale a . Luego se busca el valor de 0.005 en el primer renglón con 14 grados de libertad y se obtiene un valor de t = 2.977, pero como el valor de  está en el extremo izquierdo de la curva entonces la respuesta es t = -2.977 por lo tanto:

P(-2.977 < t < -1.761) = 0.045

Ejemplo:
Un ingeniero químico afirma que el rendimiento medio de la población de cierto proceso en lotes es 500 gramos por milímetro de materia prima. Para verificar esta afirmación toma una muestra de 25 lotes cada mes. Si el valor de t calculado cae entre –t_0.05 y t_0.05, queda satisfecho con su afirmación. ¿Qué conclusión extraería de una muestra que tiene una media de 518 gramos por milímetro y una desviación estándar de 40 gramos? Suponga que la distribución de rendimientos es aproximadamente normal.

Solución:
De la tabla encontramos que t_0.05 para 24 grados de libertad es de 1.711. Por tanto, el fabricante queda satisfecho con esta afirmación si una muestra de 25 lotes rinde un valor t entre –1.711 y 1.711.
Se procede a calcular el valor de t:

Este es un valor muy por arriba de 1.711. Si se desea obtener la probabilidad de obtener un valor de t con 24 grados de libertad igual o mayor a 2.25 se busca en la tabla y es aproximadamente de 0.02. De aquí que es probable que el fabricante concluya que el proceso produce un mejor producto del que piensa.

INTERVALO DE CONFIANZA PARA ; CON  DESCONOCIDA

ji cuadrada

En primer lugar usaremos el estadístico ji-cuadrado para probar la asociación entre dos variables, y luego lo usaremos para evaluar en qué medida se ajusta la distribución de frecuencias obtenida con los datos de una muestra, a una distribución teórica o esperada.

En términos generales, esta prueba contrasta frecuencias observadas con las frecuencias esperadas de acuerdo con la hipótesis nula. Al igual que en el caso de las pruebas anteriormente presentadas, ilustraremos con ejemplos.

Ji- cuadrado como prueba de asociación

Supongamos que un investigador está interesado en evaluar la asociación entre uso de cinturón de seguridad en vehículos particulares y el nivel socioeconómico del conductor del vehículo. Con este objeto se toma una muestra de conductores a quienes se clasifica en una tabla de asociación, encontrando los siguientes resultados:

Uso de cinturón	Nivel socioeconómico bajo	Nivel socioeconómico medio	Nivel socioeconómico alto	TOTAL
SI	8	15	28	51
NO	13	16	14	43
TOTAL	21	31	42	94

Tabla I. Tabla de asociación, valores observados.

¿Permiten estos datos afirmar que el uso del cinturón de seguridad depende del nivel socioeconómico? Usaremos un nivel de significación alfa=0,05.

Los pasos del análisis estadístico en este caso son los siguientes:

1. En primer lugar se debe plantear las hipótesis que someteremos a prueba

H0: “El uso de cinturón de seguridad es independiente del nivel socioeconómico”.
H1: “El uso de cinturón de seguridad depende del nivel socioeconómico”.

En esta prueba estadística siempre la hipótesis nula plantea que las variables analizadas son independientes.

2. En segundo lugar, obtener (calcular) las frecuencias esperadas

Estas son las frecuencias que debieran darse si las variables fueran independientes, es decir, si fuera cierta la hipótesis nula.

Las frecuencias esperadas se obtendrán de la distribución de frecuencias del total de los casos, 51 personas de un total de 94 usan el cinturón y 43 de 94 no lo usan. Esa misma proporción se debería dar al interior de los tres grupos de nivel socioeconómico, de manera que el cálculo responde al siguiente razonamiento: si de 94 personas 51 usan cinturón; de 21 personas, ¿cuántas debieran usarlo?

La respuesta a esta pregunta se obtiene aplicando la “regla de tres” y es 11,4. Este procedimiento debe repetirse con todas las frecuencias del interior de la tabla.

El detalle de los cálculos es el siguiente:

Nivel bajo: (21x51/94)=11,4-(21x43/94)=9,6
Nivel medio: (31x51/94)=16,8-(31x43/94)=14,2
Nivel alto: (42x51/94)=22,8-(42x43/94)=19,2

Estas son las frecuencias que debieran presentarse si la hipótesis nula fuera verdadera y, por consiguiente, las variables fueran independientes.

Estos valores los anotamos en una tabla con las mismas celdas que la anterior; así tendremos una tabla con los valores observados y una tabla con los valores esperados, que anotaremos en cursiva, para identificarlos bien.

Uso de cinturón	Nivel bajo	Nivel medio	Nivel alto	TOTAL
SI	11,4	16,8	22,8	51
NO	9,6	14,2	19,2	43
TOTAL	21	31	42	94

Tabla II. Tabla de asociación, valores esperados.

3. En tercer lugar se debe calcular el estadístico de prueba

En este caso, el estadístico de prueba es Ji-cuadrado que, como dijimos al comienzo, compara las frecuencias que entregan los datos de la muestra (frecuencias observadas) con las frecuencias esperadas, y tiene la siguiente fórmula cálculo:

 donde o_i  representa a cada frecuencia observada y e_i representa a cada frecuencia esperada.

De este modo el valor del estadístico de prueba para este problema será:

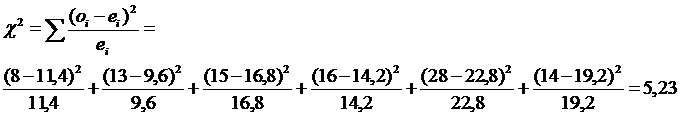
Entonces 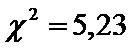 Este es el valor de nuestro estadístico de prueba que ahora, siguiendo el procedimiento de problemas anteriores (paso 4), debemos comparar con un valor de la tabla de probabilidades para ji-cuadrado (x²). Esta tabla es muy parecida a la tabla t de student, pero tiene sólo valores positivos porque ji-cuadrado sólo da resultados positivos. Véase gráfico 1, que muestra la forma de la curva, con valores desde 0 hasta infinito.

 

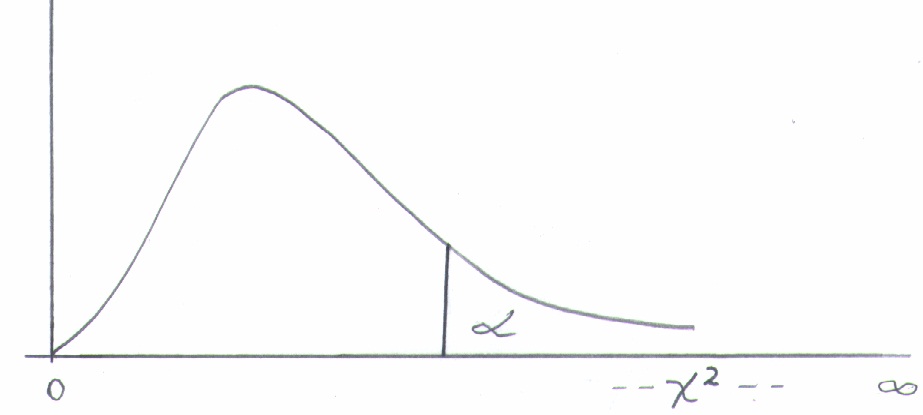
Gráfico 1.

Dado que el estadístico ji cuadrado sólo toma valores positivos, la zona de rechazo de la hipótesis nula siempre estará del lado derecho de la curva.

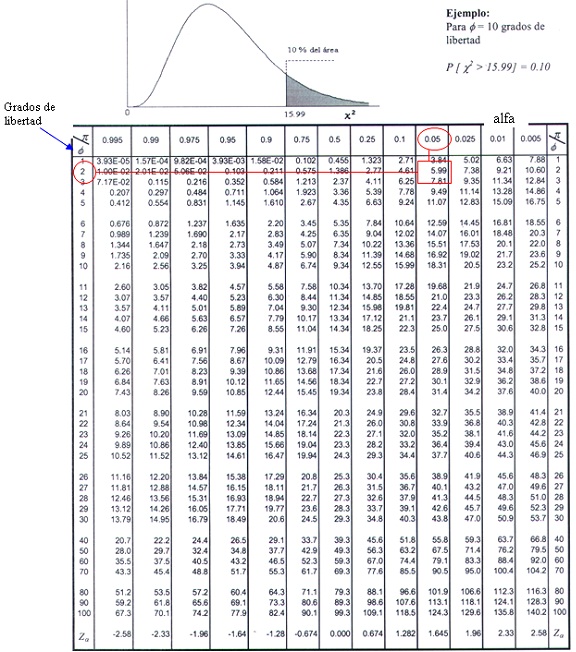
Uso de tabla ji-cuadrado

La tabla de ji-cuadrado tiene en la primera columna los grados de libertad y en la primera fila la probabilidad asociada a valores mayores a un determinado valor del estadístico (véase gráfico de la tabla III).
Los grados de libertad dependen del número de celdas que tiene la tabla de asociación donde están los datos del problema y su fórmula de cálculo es muy sencilla:

Grados de libertad (gl)=(nº de filas–1)x(nº de columnas–1)

Así, en nuestro ejemplo, en que hay 2 filas y 3 columnas, los grados de libertad serán:

gl=(2-1)x(3-1)=2

Nótese que no se consideran la fila ni la columna de los totales.