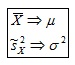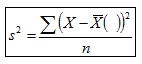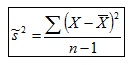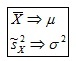Prueba de hipotesis para Varianza, Media, Proporciones

PRUEBA DE HIPÓTESIS PARA UNA VARIANZA

Pruebas de hipótesis para una varianza Es un procedimiento para juzgar si una propiedad que se supone cumple una población estadística es compatible con lo observado en una muestra de dicha población en este caso la varianza, para ello formularemos dos Hipótesis (llamada "Hipótesis Nula") y (llamada "Hipótesis Alternativa"), con ellas realizaremos una o mas pruebas, para tratar de encontrar cual deberíamos rechazar. En este procedimiento lo que buscamos es, mediante unos criterios de rechazo preestablecidos, tratar de desmentir nuestra “Hipótesis Nula” por lo cual tomaríamos la “Hipótesis alternativa”, de lo contrario no rechazaríamos nuestra ”Hipótesis Nula” y desecharíamos la ”Hipótesis. 

la función Chi cuadrado tiene una distribución de datos de la siguiente forma:

Lo que nos da a entender que a diferencia de las distribuciones normales y t Student que hemos venido trabajando, Chi cuadrado no es simétrica, es por esto que cuando hallamos los limites para una prueba de hipótesis a dos colas, debemos hallar el chi cuadrado de y ,a diferencia de las otras dos distribuciones mencionadas anteriormente, en las cuales solo era necesario calcular uno de estos valores y el otro limite se conocería multiplicando el hallado por 1. A continuación enseñaremos a manejar la tabla de la distribución Chi cuadrado. En esta nos dan dos parámetros, el primero es en el que nos relaciona con , y el segundo que representa los grados de libertad, para efectos prácticos, en la tabla se busca de la siguiente forma:

PRUEBA DE HIPOTESIS PARA MEDIAS

En vez de estimar el valor de un parámetro, a veces se debe decidir si una afirmación relativa a un parámetro es verdadera o falsa. Es decir, probar una hipótesis relativa a un parámetro. Se realiza una prueba de hipótesis cuando se desea probar una afirmación realizada acerca de un parámetro o parámetros de una población.

Una hipótesis es un enunciado acerca del valor de un parámetro (media, proporción, etc.).

Prueba de Hipótesis es un procedimiento basado en evidencia muestral (estadístico) y en la teoría de probabilidad (distribución muestral del estadístico) para determinar si una hipótesis es razonable y no debe rechazarse, o si es irrazonable y debe ser rechazada.

La hipótesis de que el parámetro de la población es igual a un valor determinado se conoce como hipótesis nula. Una hipótesis nula es siempre una de status quo o de no diferencia.

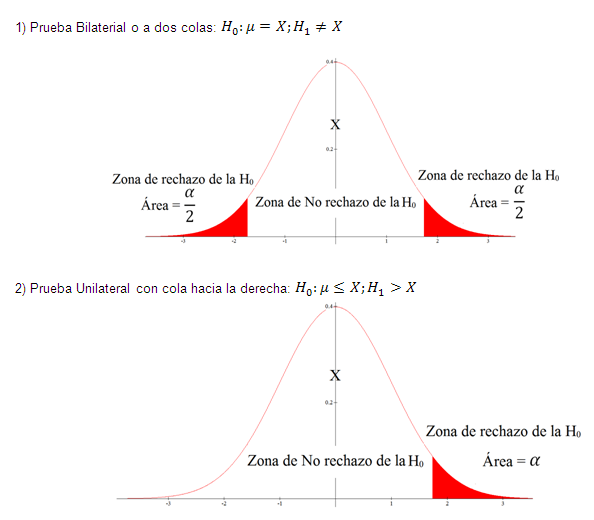
En toda prueba de hipótesis se presentan 3 casos de zonas críticas o llamadas también zonas de rechazo de la hipótesis nula, estos casos son los siguientes:

En toda prueba de hipótesis se pueden cometer 2 tipos de errores:

Prueba medias de una muestra

Se utiliza una prueba de una muestra para probar una afirmación con respecto a una media de una población única.

Nota: Se considera práctico utilizar la distribución t solamente cuando se requiera que el tamaño de la muestra sea menor de 30, ya que para muestras más grandes los valores t y z son aproximadamente iguales, y es posible emplear la distribución normal en lugar de la distribución t.

Ejemplos ilustrativos:

1) La duración media de una muestra de 300 focos producidos por una compañía resulta ser de 1620 horas.

Como se tiene como dato el tamaño de la población se tiene que verificar si cumple con la condición para utilizar el factor finito de corrección.

Los cálculos en Excel se muestran en la siguiente imagen:

El gráfico elaborado con Winstats y Paint se muestra en la siguiente imagen:

2) La duración media de lámparas producidas por una compañía han sido en el pasado de 1120 horas. Una muestra de 8 lámparas de la producciónactual dio una duración media de 1070 horas con una desviación típica de 125 horas.

Los cálculos en Excel se muestran en la siguiente imagen:

El gráfico elaborado con Winstats y Paint se muestra en la siguiente imagen:

Prueba medias de dos muestras

Las pruebas de dos muestras se utilizan para decidir si las medias de dos poblaciones son iguales. Se requieren dos muestras independientes, una de cada una de las dos poblaciones. Considérese, por ejemplo, una compañía investigadora que experimentan con dos diferentes mezclas de pintura, para ver si se puede modificar el tiempo de secado de una pintura para uso doméstico. Cada mezcla es probada un determinado número de veces, y comparados posteriormente los tiempos medios de secado de las dos muestras. Una parece ser superior, ya que su tiempo medio de secado (muestra) es 30 minutos menor que el de la otra muestra.

Pero, ¿son realmente diferentes los tiempos medios de secado de las dos pinturas, o esta diferencia muestral es nada más la variación aleatoria que se espera, aun cuando las dos fórmulas presentan idénticos tiempos medios de secado? Una vez más, las diferencias casuales se deben distinguir de las diferencias reales.

Con frecuencia se utilizan pruebas de dos muestras para comparar dos métodos de enseñanza, dos marcas, dos ciudades, dos distritos escolares y otras cosas semejantes.

La hipótesis nula puede establecer que las dos poblaciones tienen medias iguales:

Para tamaños más pequeños de muestra, Z estará distribuida normalmente sólo si las dos poblaciones que se muestrean también lo están.

Ejemplo ilustrativo

La media de las calificaciones de dos muestras de 15 estudiantes de primer semestre en la asignatura de Estadística de la universidad UTN resulta ser de 7 y 8,5. Se sabe que la desviación típica de las calificaciones en esta asignatura fue en el pasado de 1,5.

Los cálculos en Excel se muestran en la siguiente figura:

PRUEBA DE HIPÓTESIS PARA PROPORCIONES

El procedimiento para la prueba de hipótesis de proporciones es el siguiente:

1.     Especifica la hipótesis nula y alternativa.

Hipótesis Nula:

Hipótesis Alternativa: ,

donde P = la proporción de clientes con ingresos familiares anuales de $200,000 o más.

2.     Específica el nivel de significación, , permitido. Para una , el valor de tabla de Z para una prueba de una sola cola  es igual a 1.64.

3.     Calcula el error estándar de la proporción específicada en la hipótesis nula.

donde:

p = proporción especificada en la hipótesis nula.

n = tamaño de la muestra.

Por consiguiente:

4.     Calcula la estadística de prueba:

5.     La hipótesis nula se rechaza porque el valor de la Z calculada es mayor que el valor crítico Z . El banco puede concluir con un 95 por ciento de confianza  que más de un 60 por ciento de sus clientes tienen ingresos familiares de $200,000 o más. La administración puede introducir el nuevo paquete de servicios orientado a este grupo.

intervalo de confianza para la varianza

Intervalo de confianza para la varianza de una distribución Normal

Dada una variable aleatoria con distribución Normal N(μ; σ), el objetivo es la construcción de un intervalo de confianza para el parámetro σ, basado en una muestra de tamaño n de la variable. 

A partir del estadístico

la fórmula para el intervalo de confianza, con nivel de confianza 1 − α es la siguiente

Donde χ²_α/2 es el valor de una distribución ji-cuadrado con n − 1 grados de libertad que deja a su derecha una probabilidad de α/2.

Por ejemplo, dados los datos siguientes:

• Distribución poblacional: Normal
• Tamaño de muestra: 10
• Confianza deseada para el intervalo: 95 %
• Varianza muestral corregida: 38,5

Un intervalo de confianza al 95 % para la varianza de la distribución viene dado por:

que resulta, finalmente

Estimadores Media poblacional

Estimadores
Ejercicio en clases
25+15.53.88=40.5388
25-15.5388=9.4612

9.4612<M<40.5388

ESTIMADORES

 Características estimadores

1) Sesgo. Se dice que un estimador es insesgado si la Media de la distribución del estimador es igual al parámetro.

Estimadores insesgados son la Media muestral (estimador de la Media de la población) y la Varianza (estimador de la Varianza de la población):

Ejemplo

En una población de 500 puntuaciones cuya Media (m) es igual a 5.09 han hecho un muestreo aleatorio (número de muestras= 10000, tamaño de las muestras= 100) y hallan que la Media de las Medias muestrales es igual a 5.09, (la media poblacional y la media de las medias muestrales coinciden). En cambio, la Mediana de la población es igual a 5 y la Media de las Medianas es igual a 5.1 esto es, hay diferencia ya que la Mediana es un estimador sesgado.

La Varianza es un estimador sesgado. Ejemplo: La Media de las Varianzas obtenidas con la Varianza

en un muestreo de 1000 muestras (n=25) en que la Varianza de la población es igual a 9.56ha resultado igual a 9.12, esto es, no coinciden. En cambio, al utilizar la Cuasivarianza

la Media de las Varianzas muestrales es igual a 9.5, esto es, coincide con la Varianza de la población ya que la Cuasivarianza es un estimador insesgado.

2) Consistencia. Un estimador es consistente si aproxima el valor del parámetro cuanto mayor es n (tamaño de la muestra).

Algunos estimadores consistentes son:

Ejemplo

En una población de 500 puntuaciones cuya Media (m) es igual a 4.9 han hecho tres muestreos aleatorios (número de muestras= 100) con los siguientes resultados:

vemos que el muestreo en que n=100 la Media de las Medias muestrales toma el mismo valor que la Media de la población.

3) Eficiencia. Diremos que un estimador es más eficiente que otro si la Varianza de la distribución muestral del estimador es menor a la del otro estimador. Cuanto menor es la eficiencia, menor es la confianza de que el estadístico obtenido en la muestra aproxime al parámetro poblacional.

Ejemplo

La Varianza de la distribución muestral de la Media en un muestreo aleatorio (número de muestras: 1000, n=25) ha resultado igual a 0.4. La Varianza de la distribución de Medianas ha resultado, en el mismo muestreo, igual a 1.12, (este resultado muestra que la Media es un estimador más eficiente que la Mediana).

DISTRIBUCION DE T DE STUDENT

DISTRIBUCION "T DE STUDENT"

Supóngase que se toma una muestra de una población normal con media  y varianza . Si es el promedio de las n observaciones que contiene la muestra aleatoria, entonces la distribución  es una distribución normal estándar. Supóngase que la varianza de la población ² es desconocida. ¿Qué sucede con la distribución de esta estadística si se reemplaza  por s? La distribución t proporciona la respuesta a esta pregunta.

La media y la varianza de la distribución t son  = 0 y  para >2, respectivamente.

La siguiente figura presenta la gráfica de varias distribuciones t. La apariencia general de la distribución t es similar a la de la distribución normal estándar: ambas son simétricas y unimodales, y el valor máximo de la ordenada se alcanza en la media  = 0. Sin embargo, la distribución t tiene colas más amplias que la normal; esto es, la probabilidad de las colas es mayor que en la distribución normal. A medida que el número de grados de libertad tiende a infinito, la forma límite de la distribución t es la distribución normal estándar.

Propiedades de las distribuciones t

1. Cada curva t tiene forma de campana con centro en 0.



2. Cada curva t, está más dispersa que la curva normal estándar z.


3. A medida que  aumenta, la dispersión de la curva t correspondiente disminuye.


4. A medida que  , la secuencia de curvas t se aproxima a la curva normal estándar, por lo que la curva z recibe a veces el nombre de curva t con gl = 

La distribución de la variable aleatoria t está dada por:

Esta se conoce como la distribución t con  grados de libertad.

Sean X₁, X₂, . . . , X_n variables aleatorias independientes que son todas normales con media  y desviación estándar . Entonces la variable aleatoria  tiene una distribución t con  = n-1 grados de libertad.

La distribución de probabilidad de t se publicó por primera vez en 1908 en un artículo de W. S. Gosset. En esa época, Gosset era empleado de una cervecería irlandesa que desaprobaba la publicación de investigaciones de sus empleados. Para evadir esta prohibición, publicó su trabajo en secreto bajo el nombre de "Student". En consecuencia, la distribución t normalmente se llama distribución t de Student, o simplemente distribución t. Para derivar la ecuación de esta distribución, Gosset supone que las muestras se seleccionan de una población normal. Aunque esto parecería una suposición muy restrictiva, se puede mostrar que las poblaciones no normales que poseen distribuciones en forma casi de campana aún proporcionan valores de t que se aproximan muy de cerca a la distribución t.

La distribución t difiere de la de Z en que la varianza de t depende del tamaño de la muestra y siempre es mayor a uno. Unicamente cuando el tamaño de la muestra tiende a infinito las dos distribuciones serán las mismas.

Se acostumbra representar con el valor t por arriba del cual se encuentra un área igual a . Como la distribución t es simétrica alrededor de una media de cero, tenemos; es decir, el valor t que deja un área de  a la derecha y por tanto un área de  a la izquierda, es igual al valor t negativo que deja un área de  en la cola derecha de la distribución. Esto es, t_0.95 = -t_0.05, t_0.99=-t_0.01, etc.

Para encontrar los valores de t se utilizará la tabla de valores críticos de la distribución t del libro Probabilidad y Estadística para Ingenieros de los autores Walpole, Myers y Myers.

Ejemplo:

El valor t con  = 14 grados de libertad que deja un área de 0.025 a la izquierda, y por tanto un área de 0.975 a la derecha, es

t_0.975=-t_0.025 = -2.145

Si se observa la tabla, el área sombreada de la curva es de la cola derecha, es por esto que se tiene que hacer la resta de . La manera de encontrar el valor de t es buscar el valor de  en el primer renglón de la tabla y luego buscar los grados de libertad en la primer columna y donde se intercepten  y  se obtendrá el valor de t.

Ejemplo:
Encuentre la probabilidad de –t_0.025 < t < t_0.05.
Solución:

Como t_0.05 deja un área de 0.05 a la derecha, y –t_0.025 deja un área de 0.025 a la izquierda, encontramos un área total de 1-0.05-0.025 = 0.925.

P( –t_0.025 < t < t_0.05) = 0.925

Ejemplo:
Encuentre k tal que P(k < t < -1.761) = 0.045, para una muestra aleatoria de tamaño 15 que se selecciona de una distribución normal.
Solución:

Si se busca en la tabla el valor de t =1.761 con 14 grados de libertad nos damos cuenta que a este valor le corresponde un área de 0.05 a la izquierda, por ser negativo el valor. Entonces si se resta 0.05 y 0.045 se tiene un valor de 0.005, que equivale a . Luego se busca el valor de 0.005 en el primer renglón con 14 grados de libertad y se obtiene un valor de t = 2.977, pero como el valor de  está en el extremo izquierdo de la curva entonces la respuesta es t = -2.977 por lo tanto:

P(-2.977 < t < -1.761) = 0.045

Ejemplo:
Un ingeniero químico afirma que el rendimiento medio de la población de cierto proceso en lotes es 500 gramos por milímetro de materia prima. Para verificar esta afirmación toma una muestra de 25 lotes cada mes. Si el valor de t calculado cae entre –t_0.05 y t_0.05, queda satisfecho con su afirmación. ¿Qué conclusión extraería de una muestra que tiene una media de 518 gramos por milímetro y una desviación estándar de 40 gramos? Suponga que la distribución de rendimientos es aproximadamente normal.

Solución:
De la tabla encontramos que t_0.05 para 24 grados de libertad es de 1.711. Por tanto, el fabricante queda satisfecho con esta afirmación si una muestra de 25 lotes rinde un valor t entre –1.711 y 1.711.
Se procede a calcular el valor de t:

Este es un valor muy por arriba de 1.711. Si se desea obtener la probabilidad de obtener un valor de t con 24 grados de libertad igual o mayor a 2.25 se busca en la tabla y es aproximadamente de 0.02. De aquí que es probable que el fabricante concluya que el proceso produce un mejor producto del que piensa.

INTERVALO DE CONFIANZA PARA ; CON  DESCONOCIDA